Special Kinds of Matrices and Vectors

Notes from Deep Learning by Ian Goodfellow, Yoshua Bengio, and Aaron Courville

Posted by Bhagya C on February 9, 2021

Following are some matrices and vectors which are useful for understanding deep learning concepts

  • Diagonal Matrix 

Matrices, in which all elements are zero except in the main diagonal line

ie: Dij = 0 for all i≭j

The identity matrix is a diagonal matrix where all the elements are 1

diag(v) means a diagonal matrix whose diagonal elements are denoted by a vector

The good characteristics of the diagonal matrices are their computational efficiency on multiple actions

  • eg) diag(v)x = v๏x also the inverse of diag(v) is also efficient
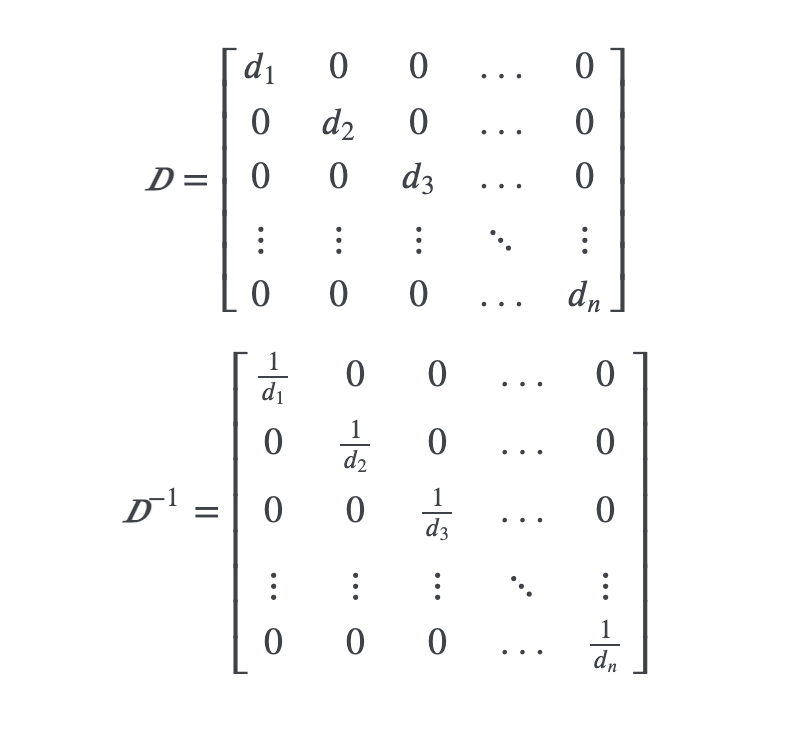    •  Inverse of Diagonal matrix

    While deriving machine learning algorithms we can restrict matrices to diagonal and make the process less expensive as well as descriptive

    There are rectangular diagonal matrices as well.Albeit they don’t have an inverse, matrix multiplication is cheaper as scaring the matrix by x time ( either making it more taller or wider by a factor of x) in Dx

    • Symmetric Matrix

    When a matrix is equal to its transpose it is known as symmetric. 

    Symmetric Matrix is created by functions with two arguments and was the order of arguments wont affect the final result ( also known as a symmetric function)

    • Unit vector

    Unit vector is a vector with unit norm 

    some back ground information about norms - norms are function we use to measure the size of the vector. The norms with Lp are functions mapping vectors into a non-negative values

    L2 is known as Euclidean norm

    • Orthogonal vector

    If two vectors are orthogonal to each other then XTY = 0

    If both the vectors have a non zero norm then it means there are perpendicular to each other. If two vectors are not only perpendicular to each other and has a unit norm then they known as orthonormal

    An orthogonal matrix is a square matrix whose rows are mutually orthonormal and whose columns are mutually orthonormal

                A-1 = AT

    As the inverse of the orthogonal vectors are very cheap to compute they have very much demand ( side note : as we know inorder to solve the problems like finding weights of the features, we need to solve the equation. Where the most challenging part of that is finding the inverse of the matrix, whereas the features are orthogonal it is very easy)